Chapter 11 Writing functions in R
In this section we will be learning some more advanced topics in R which will let us write more complex scripts and carry out more difficult tasks. This is where we will start treating R as a proper programming language. If you mostly use computers for word processing, surfing the web and so on you might only have a vague understanding of what programming is, and if you’re like a lot of people you might regard it as a complicated and obscure activity mainly pursued by socially dysfunctional refugees from Big Bang Theory. If that’s you, then I’ve got some news - if you’ve made it through the book to here then you’ve already been writing short programmes and running them in R. What is a computer programme? It’s some code put together to produce some kind of output and clearly that’s what you’ve been producing already in the form of R scripts. Dinner with Penny (or Sheldon if you prefer) awaits.
R is fundamentally a programming language that happens to be particularly useful for analysing and visualising data. If you just want to do some statistical testing and draw some graphs to display your data, then you can think of R as simply being a piece of data analysis software that you control by typing in commands. That’s probably all that a lot of people need, and if that’s the case for you then it’s probably best to skip this part of the book, or perhaps come back to it later. One of the the strengths of R, however, is that it allows you to string all of that code together into programmes (up until now we’ve been calling these ‘scripts’) which will allow you to do whatever complex operations on your data you might choose. If you want to start going beyond just using the built in functions to do single analyses or draw graphs one at a time with your data then this section of the book is for you. We’ll start by looking at how you can write your own functions.
11.1 Writing functions
So far we’ve just used the functions in R without spending any time thinking about how they work, how they were written or whether we could write our own. You might have been regarding them as something of a black box - a thing you can control that does what you want it to but which does it by some form of magic. It’s time to get rid of that stereotype: once you understand how R code works, functions in R are easy to write - in fact, if you want to write your own function you can simply define it like an R object using the function function(). The basic layout for a new function looks like this.
function.name <-
function(argument,
next.argument) {
Some code that does whatever you want done with the arguments
}You’ve already seen how functions in R can take one or more arguments to control exactly what the function produces. If you want to write your own function then the arguments for your new function are simply specified as the arguments for the eponymous function() function. If you want to include an argument with no default value then you just put the name you want to use, and if you want to set a default value then you can specify this by setting the argument equal to whatever value you want.
function.name <-
function(argument,
next.argument = 25,
more.arguments = TRUE) {
Some code that does whatever you want done with the arguments
}Here we have three arguments for our function. The first one has no default value, the second is a numeric argument and has the default value of 25 and the third is a logical argument and has a default value of TRUE. Arguments with no default value are often used when you want your function to work on an object such as a vector, a matrix, a data frame or the saved output of another function.
One thing you might not have seen before are the braces that come after the function call and the set of new argument in ordinary brackets. These curly brackets are something that you’ll see a lot of in R code being used to group sets of expressions. When you give R a set of instructions in braces it will carry out each instruction in turn but when it gets to the closing brace it will only return the results of the last instruction it carried out. Here’s an example: note that this isn’t a function, this is just getting R to carry out a series of instructions.
sim.data <- {
sim.data <- runif(10, 0, 10)
sim.data <- sim.data + rnorm(10, 0, 1)
round(sim.data, 1)
}Here I’ve put three expressions in the braces - firstly generate ten uniformly distributed random numbers between 0 and 10 using the runif() function, then add another random number drawn from a standard normal distribution to each number, and finally round them all off to one decimal place. If you type this directly into an R console you’ll notice that as you enter each line R adds a + sign once you’ve pressed “enter” - this is just to let you know that it can’t yet carry out the instructions until we put in the closing brace. What we end up with, stored as the object sim.data, is the result of the last expression in the braces.
sim.data
[1] 4.9 10.0 8.9 1.0 7.6 3.4 1.1 7.6 0.1 9.2Using braces to define your function means that you can use as many lines of code as you like and do as many calculations as you like in your function, and then end up with the result you want rather than a pile of other unnecessary variables and other objects that you might have set up to make the calculations for the function work.
11.1.1 Simple functions
It’s best to show how this works with some examples. Here’s a very simple function: this simply takes a vector as an argument and divides each number by 10. There is only one argument which we’ll call x.
divider <- function(x) {
x/10
}Let’s check if it works.
X1 <- c(5,10,50, 100)
divider(X1)
[1] 0.5 1.0 5.0 10.0That looks fine. If we want to make the function a bit more flexible we can add a second argument that specifies the number we want our vector to be divided by.
divider <- function(x, div = 10) {
x/div
}Now we have two arguments for our function. The first, x is whatever vector we input to the function and the second, div is the number we’d like our vector to be divided by. Notice that we have set a default value for div of 10, so if we don’t set a value then the default operation will be division by 10. Here’s how to use our new function to divide all the numbers in a vector by 2
X1 <- c(5,10,50, 100)
divider(X1, div = 2)
[1] 2.5 5.0 25.0 50.011.1.2 Calculating confidence intervals
Here’s a more complex example. This function takes a vector of numbers and calculates the mean and 95% confidence intervals of that vector. If you don’t know what confidence intervals are, they are a way of telling how confident we can be in a calculated mean: so larger confidence intervals mean that we’re less sure. The actual calculation is a bit complex and I won’t explain it in detail: if you want to know more then there is a full explanation in the Introductory Biostatistics in R book.
meanci <- function(X1) {
lenX1 <- length(X1)
X195 <- qt(0.975, df = lenX1 - 1) * sd(X1) / sqrt(lenX1)
output <- c(Lower.CI = mean(X1) - X195,
Upper.CI = mean(X1) + X195)
output
}Let’s go through that line-by-line.
meanci <- function(X1) {
}Here we use the allocation symbol to set up a new object called “meanci.” We tell R that meanci is a function, and it only has one argument, “X1,” which has no default value. We then close the brackets on the list of arguments and finish with an opening brace { which tells R that everything from then on until the braces are closed } is the code that meanci should use.
lenX1 <- length(X1)Now we’re looking at the code that the function will use. The first line just calculates the length of the vector X1.
X195 <- qt(0.975, df = lenX1 - 1) * sd(X1) / sqrt(lenX1)The next line calculates the confidence interval. You can see that lenX1 apears a couple of times because the sample size is needed for this calculation.
output <- c(Lower.CI = mean(X1) - X195,
Upper.CI = mean(X1) + X195)This calculates the upper and lower 95% confidence bounds by adding and subtracting our value from the mean, and puts the calculated values into a vector with a name for each one to make sure you know which is which.
output
}The last thing we do before closing our braces is to put the name of the object that we want as the output from the function, in this case output. The closing brace tells R that the block of code that should be run for the function is finished. Does it work?
test <- rnorm(50, 12, 3)Sets up a vector of 50 numbers drawn randomly from a normal distribution with a mean of 12 and a standard deviation of 3.
meanci(test)
Lower.CI Upper.CI
11.632 13.463 This does indeed give us the 95% confidence intervals for the mean for our vector test.
11.1.3 Adding an argument
Our function only calculates the 95% confidence intervals: we might want the 99% or 90% intervals instead. We can add in another argument that let’s the user choose the confidence level they want. Let’s call it conf.
meanci <- function(X1, conf = 95) {
}The function now has two arguments, and the second one has a default value assigned: if the user doesn’t give a value for conf, then the function will assume it should produce the 95% intervals.
meanci <- function(X1, conf = 95) {
lenX1 <- length(X1)
X195 <-
qt(1 - (100 - conf) / 200, df = lenX1 - 1) * sd(X1) / sqrt(lenX1)
output <- c(Lower.CI = mean(X1) - X195,
Upper.CI = mean(X1) + X195)
output
}Here is our new function. The calculation of the size of the confidence interval is now more complicated because instead of just calculating the 95% confidence interval we’re being more flexible, so the code takes the value for “conf” and does a bit of arithmetic with that to obtain the necessary value of t. Another thing to note is that we’ve lost the return() function from the last line - now it just gives the name of the object. Most of the time you don’t actually need to specify that something should be “returned” - just giving the name of the object is enough.
test2<-rnorm(50,10,2)Here’s a new test vector, 50 random numbers drawn from a normal distribution with mean 10 and standard deviation 2.
meanci(test2, conf=95)
Lower.CI Upper.CI
9.4746 10.5573
meanci(test2, conf=66)
Lower.CI Upper.CI
9.7564 10.2755 That seems to work just fine — you can see that the 66% confidence intervals are narrower than the 95% ones.
11.2 Exercises
Write a function that will take a number, multiply it by two and then return the square of the product: in other words, a function that will calculate \(\left( x \times 2 \right) ^2\)
Test it on a vector of 5 random numbers drawn from a standard normal distribution with mean zero and standard deviation 1
Now add an argument called power to the function that enables the user to specify the power that the product should be raised to - i.e. instead of squaring the sum of the number and 5, add something that will allow the user to raise it to the power 2 or 5 or 0.8. Make the default value of power equal to 2. Test it on your vector of random numbers again with the values 5 and 0.5.
Now add an argument called “multiply” that will let the user choose the amount to multiply the number by, so instead of multiplying by 2 the user can decide to multiply by 0.1 or 2 or -28. Set the default value as 2 again and test it on your random numbers again with the values 0.1 and -28, and with the default value for power.
Use the
seq()function to set up a vector called “X” with a sequence of 400 numbers from -12 to 12. Use this and your function to plot a graph showing the function
\[y = \left( \frac{x}{10} \right) ^z\]
from x=-10 to x=10 and for the following values of z: 1,2,3.
11.3 Solutions to exercises
- Write a function that will take a number, multiply it by two and then return the square of the product: in other words, a function that will calculate \(\left( x \times 2 \right) ^2\)
myfunction <- function(X) {
(X * 2) ^ 2
}
# NB because there is only one line of instructions we
# could have missed out the braces and just put the
# calculation on the same line as the name of the
# function. I've included the braces here for consistency
# with the rest of the book. - Test it on a vector of 5 random numbers drawn from a standard normal distribution with mean zero and standard deviation 1
test <- rnorm(5, 0, 1)
myfunction(test)
[1] 0.0067216 0.7586771 2.8120890 2.9261981 9.0841087- Now add an argument called power to the function that enables the user to specify the power that the product should be raised to - i.e. instead of squaring the sum of the number and 5, add something that will allow the user to raise it to the power 2 or 5 or 0.8. Make the default value of power equal to 2. Test it on your vector of random numbers again with the values 5 and 0.5.
myfunction <- function(X, power = 2) {
(X * 2) ^ power
}
myfunction(test, power = 5)
[1] -3.7041e-06 -5.0135e-01 1.3261e+01 -1.4647e+01 2.4872e+02
myfunction(test, power = 0.5)
[1] NaN NaN 1.2950 NaN 1.7361Note that when power is set to <1 you get NaN returned for the negative values in your test variable. NaN means Not a Number and is returned because you can’t calculate a power less than one for a negative number. If this is a bit confusing, remember that raising something to the power 0.5 is the same as taking the square root, and you can’t find the square root of a negative number.
- Now add an argument called “multiply” that will let the user choose the amount to multiply the number by, so instead of multiplying by 2 the user can decide to multiply by 0.1 or 2 or -28. Set the default value as 2 again and test it on your random numbers again with the values 0.1 and -28, and with the default value for power.
myfunction <- function(X, power = 2, multiply = 2) {
(X * multiply) ^ power
}
myfunction(test, multiply = 0.1)
[1] 1.6804e-05 1.8967e-03 7.0302e-03 7.3155e-03 2.2710e-02
myfunction(test, multiply = -28)
[1] 1.3174 148.7007 551.1694 573.5348 1780.4853- Use the
seq()function to set up a vector called “X” with a sequence of 400 numbers from -12 to 12. Use this and your function to plot a graph showing the function
\[y = \left( \frac{x}{10} \right) ^z\]
from x=-10 to x=10 and for the following values of z: 1,2,3.
X<-seq(-12,12,length=400)Here’s how to do this in base R graphics. You could do this by calculating a separate Y variable from X for each seperate line, but it’s simpler just to do the calculations within the plot() and points() functions. I’m also going to add a legend.
plot(
X,
myfunction(X, multiply = 0.1, power = 3),
type = "l",
col = "steelblue",
ylab = "Y"
)
# Note how I cunningly used the function which
# I know is going to have the biggest maximum
# and minimum values for the initial plot command.
# This means I can just use the default y limits
# and don't need to specify them.
points(X,
myfunction(X, multiply = 0.1, power = 1),
type = "l",
col = "darkgreen")
points(X,
myfunction(X, multiply = 0.1, power = 2),
type = "l",
col = "darkred")
legend(
"bottomright",
legend = c("Power=1", "Power=2", "Power=3"),
col = c("darkgreen", "darkred", "steelblue"),
bty = "n",
lty = 1
)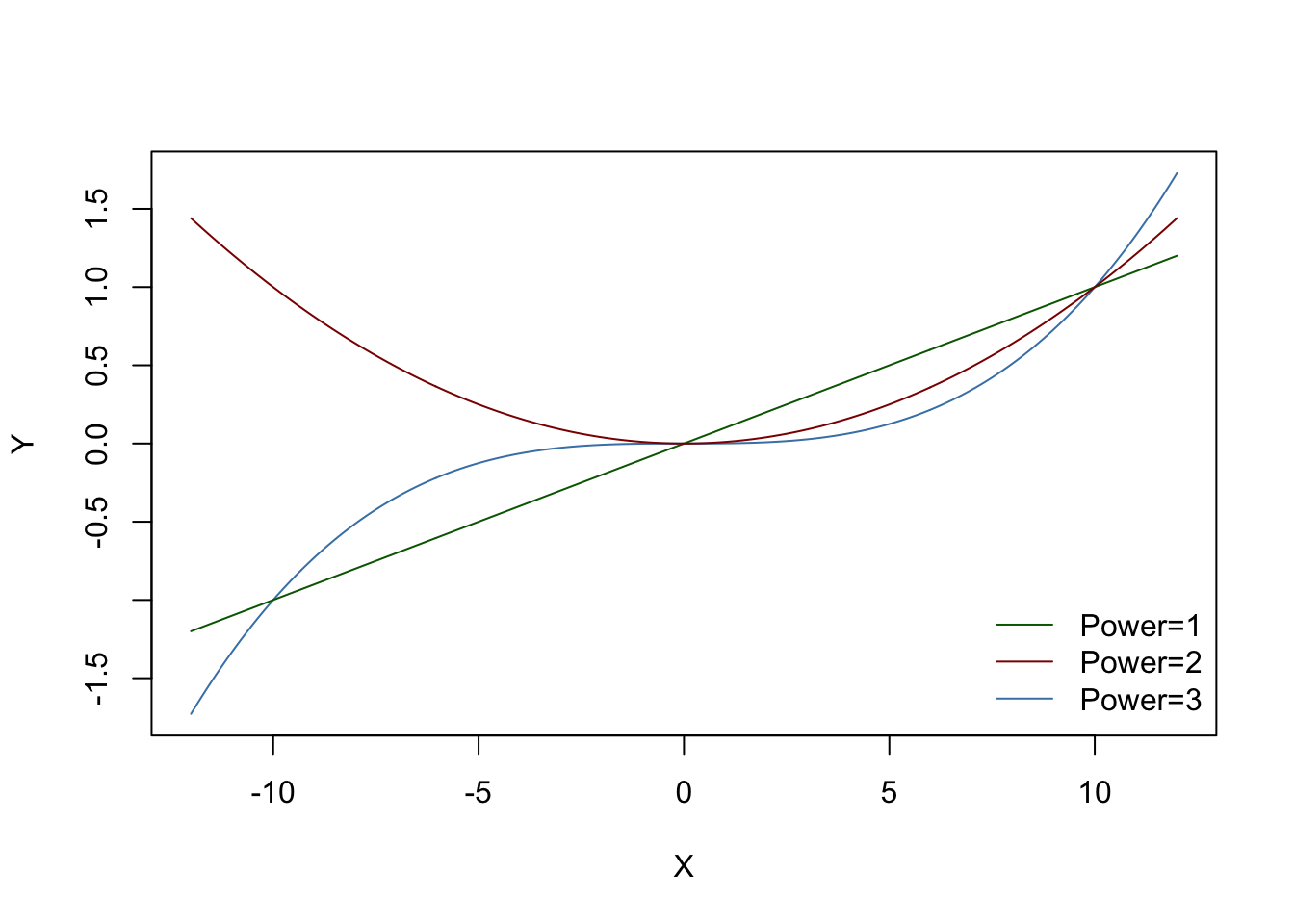
Figure 11.1: Function y=(x/10)^z plotted for values of z from 0.5 to 3
This is how to generate the same graph in ggplot2. THis time we’re going to do all the calculations first and put them in a data frame which we’ll plug into ggplot2.
library(ggplot2)
# Generate data frame
X1 <- c(X, X, X)
Power <- rep(c(1,2,3), each = 400)
Y1 <- myfunction(X1, multiply = 0.1, power = Power)
data1 <- data.frame(X1, z = as.factor(Power), Y1)
# Plot data
p1 <- ggplot(data = data1) +
aes(x = X1, y = Y1, colour = z) +
geom_line() +
theme_bw() +
labs(x = "x", y = "y")
p1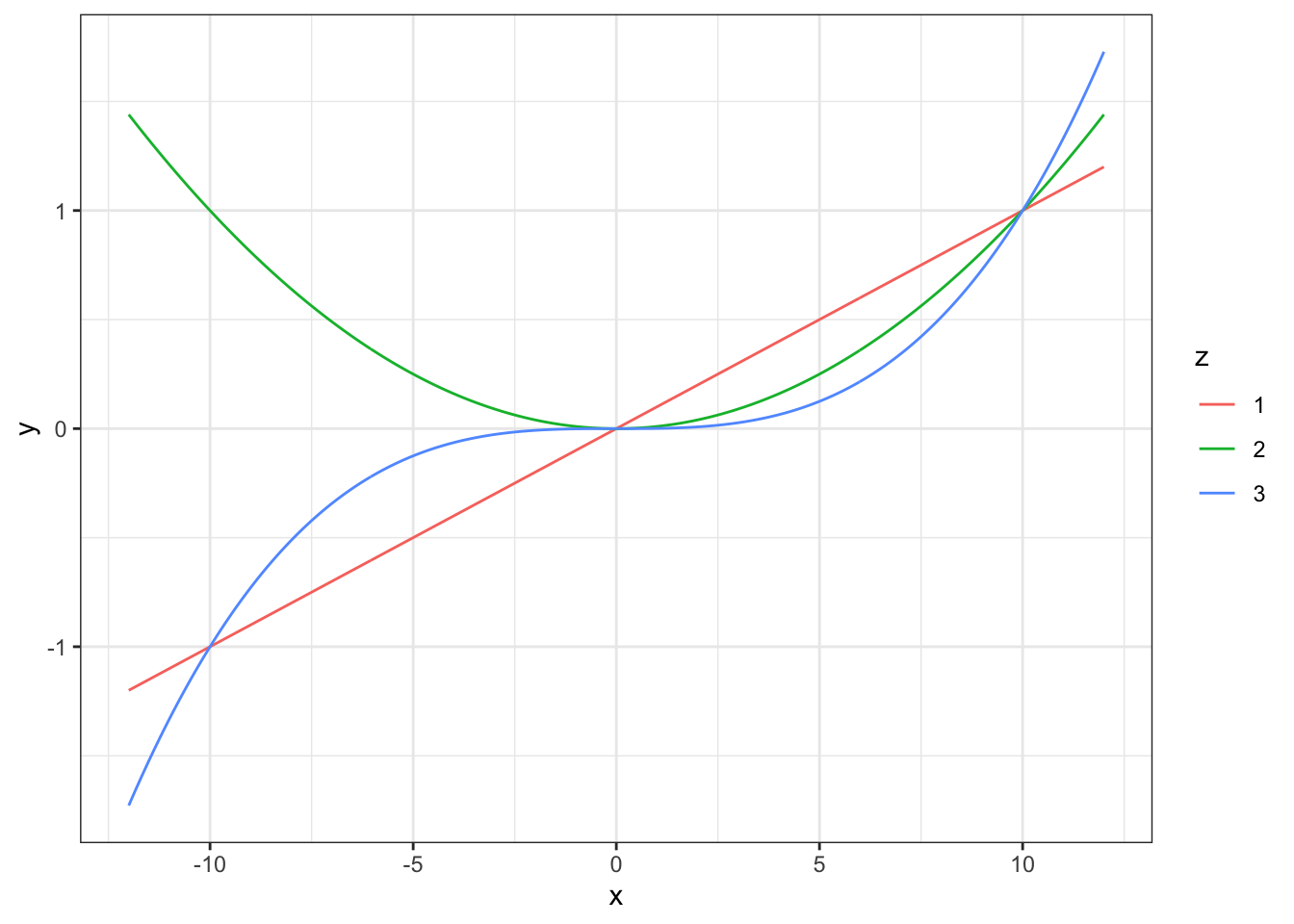
Figure 11.2: Function y=(x/10)^z plotted for values of z from 0.5 to 3