Chapter 17 Coding and Optimising Conway’s Game of Life

The “Game of Life,” originally designed by the mathematician John Conway, is a basic simulation of living cells on a two dimensional plane which is famous for its ability to produce complex behaviour from a simple set of rules. The game is set on a grid of square cells, each of which interacts with its eight neighbours, and each of which can either contain a living cell or be empty (in other words, it is a type of mathematical model called a cellular automaton). Once the initial distribution of live cells has been determined, the model proceeds as a series of discrete time steps, or generations, and every time step the fate of each living cell is determined by the number of neighbours it has.

An empty cell with three neighbouring living cells itself becomes a living cell
A live cell with one or no live neighbours dies of loneliness
A live cell with more than three live neighbours dies of overcrowding
A live cell with two or three live neighbours stays alive

I’m not going to go into detail about the history or the many fascinating behaviours that can be found in this famous model, but if you really want to understand what’s going on here you might want to read the wikipedia page on the subject or have a look around the interwebs: there’s a lot out there on the subject.

We’re going to write an R function that will run the Game of Life and then we’re going to look at ways of making the code faster. Let’s start with planning out the steps that we need to take to run the game of life.

First of all we need to set some basic parameters: what size grid will we use, how many live cells should there be to start with, and how many generations should we run the game for? These can be input by the user as arguments to our function, which also allows us to set some default values.
The next thing we need to do is to distribute our live cells for the first generation. We can do this by setting up a matrix to represent the two dimensional grid and then populating it with zeros to indicate dead cells and ones to indicate live cells.
Next, we need to work out a way of counting the number of neighbours for every cell in our grid.
Once we know how many neighbours each cell has, we can calculate what the distribution of live cells will be in the next generation on the basis of the rules above.
Since we want to do this multiple times, we need a loop going back to 3 for each generation.
It’s no good just calculating the distribution of cells for each generation. We need to see the changing pattern of living cells, so we need to draw a plot of the distribution of live cells every generation as well.

To make a more precise plan, we can visualise how our function should work by drawing a flow diagram. If you’re trying to write any sort of complex function drawing something like this can be very helpful to help work out the way the function should work, and then to help you make sure that everything’s in its place. Here’s a flow diagram for our function.

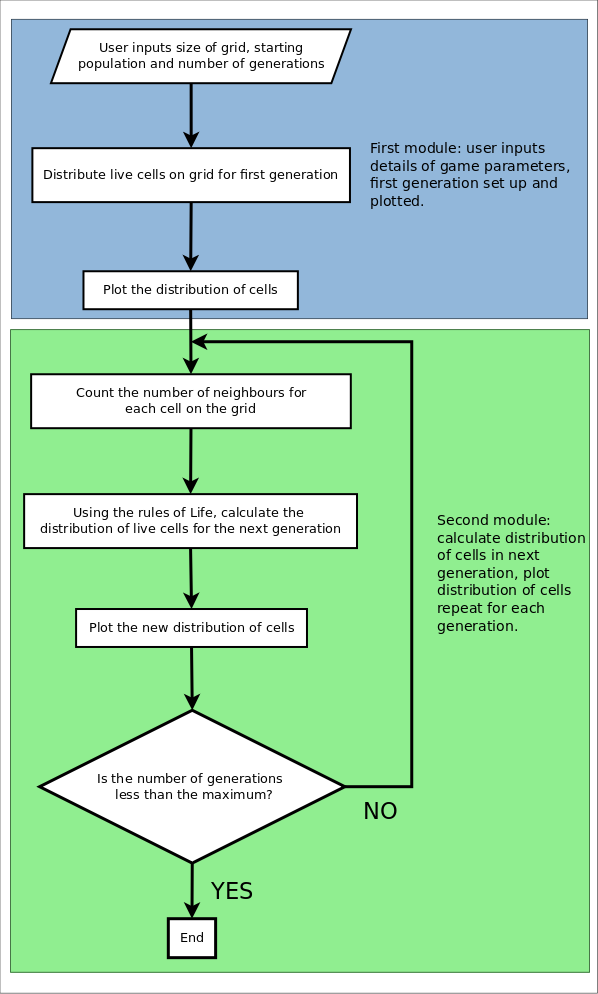
It’s often helpful to think of a programme as a series of ‘modules,’ each of which does different things. At the largest scale there are really only two ‘modules’ in this function, one which sets up the initial grid of live and dead cells, and then a second one which works out the distribution of cells in the next generation and loops back through until the simulation is finished. At a finer scale you can think of each of the boxes in the flow diagram as a separate module as well: each of them has a defined and separate function and when we put them all together we acheive what we want to do. While the basic structure of our function might be simple, however, some of the details are quite complicated: plotting the distribution of cells is not especially easy, for example, and the question of how to count the number of live neighbours for each cell is not necessarily straightforward. It’s probably best to start at the very beginning, however, (a very good place to start) rather than jumping the gun. Since we’re writing a function, we’ll start with by defining the function, its arguments and any default values that we might wish to specify.

life<-function(grid.size=12,start=50,generations=50) {
}

We’re calling our function “life” and we’ve given it three arguments, all of which come with default values. For these defaults we’ll use a grid of 12 by 12 cells, populated with 50 live cells and run it for 50 generations as default values, but remember that because we’re putting these in as arguments to the function the user will be able to use any values if they wish. Once we’ve established these basic parameters, we need to use them to set up the distribution of live cells for the first generation. There are quite a few ways to do this, but we’re going to do it by setting up a vector with ones for the live cells and zeros for the dead cells and using sample() to randomise their distribution.

init<-sample(c(rep.int(1,times=start),rep.int(0,times=(grid.size^2)-start)),size=grid.size^2,replace=FALSE)

sim.grid<-matrix(data=init,nrow=grid.size)

What this does is firstly to set up a vector which has a series of ones as long as the starting value for the population defined as start, and then a series of zeros. When added together the length of this vector is the number of cells in the grid that we are simulating the game over. We then use the sample() function to produce a new vector which has the same number of ones and zeros but with the distribution randomised, and we store this as an object called init. This then gets passed to the matrix() function in the next row to set up the distribution of live and dead cells in a matrix called sim.grid.

It’s worth noting here that this could just as easily be done in a single line of code: I put it on two lines for clarity, but you could just as easily write this:

sim.grid<-matrix(data=sample(c(rep.int(1,times=start),rep.int(0,times=(grid.size^2)-start)),size=grid.size^2,replace=FALSE),nrow=grid.size)

which many people would argue is a bit simpler and more elegant.

Now that we have the distribution of cells for our first generation, we need to get a count of how many neighbours each cell (both alive and dead) in our matrix has so that we can work out the distribution of cells for the next generation. Before we do this, we need to think a little about the boundary conditions that we want to use: what do we do if a cell is on the edge of the grid? We could use a model where the edges of the grid go nowhere, so a cell on a left-hand edge can only have neighbours above, below and to the right and a cell on a corner can only have a maximum of three neighbours. Alternatively we could use a model where the edges are looped around, so the right edge is “joined” to the left edge and a cell on the left edge can have cells on the right edge counted as neighbours and vice-versa, and the bottom is “joined” to the top such that a cell on the top edge can have cells on the bottom edge as its neighbours and vice-versa. This is actually mathematically equivalent to running our simulation on a torus: a doughnut shaped surface (ring doughnut not jam doughnut in case you were wondering, which is a shame because all right-thinking folks prefer jam doughnuts). We’re going to go for the option of running it on a torus, with wrap-around edges. This makes it a little more complicated but not desperately so.

To do these neighbour counts, we’re going to write a little function which will return the number of neighbours for any cell in a matrix, so long as the matrix only contains zeros and ones. It’s fundamentally really simple: just calculate the sum of all the numbers in the matrix which are in the locations around and including the cell we’re interested in, and then if the cell in question is live subtract one from the count for the cell in the middle.

neighbours<-function(R,C) {
Rs<-c(R-1,R,R+1)
Cs<-c(C-1,C,C+1)

 #what to do if it's on an edge
Rs<-ifelse(Rs==0,grid.size,Rs)
Rs<-ifelse(Rs==grid.size+1,1,Rs)
Cs<-ifelse(Cs==0,grid.size,Cs)
Cs<-ifelse(Cs==grid.size+1,1,Cs)

#count the neighbours. -1 for the one in the middle
count<-ifelse(sim.grid[R,C]==1,sum(sim.grid[Rs,Cs])-1,sum(sim.grid[Rs,Cs]))

count
}

The function takes two arguments, R and C (for “Row” and “Column”), which define the location on the matrix of the cell in question (rememebr that for matrix subsetting R uses the row number and then the column number). It then sets up two vectors each containing the row or column numbers one before and one as well as our our focal number, and then it uses those as subscripts and adds up the values in the nine cells of the matrix defined by them. If the focal cell is a live cell (=1) it subtracts one from the sum since we don’t count the cell itself as a neighbour. In order to make the count wrap around when the cell in question is on an edge or a corner we have to fiddle with it a bit which is what the series of ifelse() commands are for.

To actually get a count of neighbours for a whole matrix, we can use a couple of for() loops to cycle through each cell and produce a count for each one. We’ll put our counts in a new matrix called neighbours.mat.

neighbours.mat<-matrix(data=NA,nrow=grid.size,ncol=grid.size)

for (p in 1:grid.size){
  for (q in 1:grid.size){
    neighbours.mat[p,q]<-neighbours(R=p,C=q)
  }
}

Let’s check whether all of this works. We need to set up a matrix and then run our code so far to get a new matrix with the count of neighbours for each cell. To start with we need to give values for grid.size and start because we aren’t running our full function yet.

grid.size=8
start=30

Now we can use these to make a matrix for our first generation.

init<-sample(c(rep.int(1,times=start),rep.int(0,times=(grid.size^2)-start)),size=grid.size^2,replace=FALSE)

sim.grid<-matrix(data=init,nrow=grid.size)

Let’s use our function and our pair of nested loops to count the neighbours for each cell and then we can see whether what we get agrees with what we should get.

neighbours.mat<-matrix(data=NA,nrow=grid.size,ncol=grid.size)

for (p in 1:grid.size){
  for (q in 1:grid.size){
    neighbours.mat[p,q]<-neighbours(R=p,C=q)
  }
}

sim.grid
     [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,]    0    0    0    1    1    1    1    1
[2,]    1    0    0    1    1    0    1    1
[3,]    0    0    0    0    1    0    0    0
[4,]    0    0    0    0    1    0    1    1
[5,]    1    0    1    0    0    0    0    1
[6,]    1    1    1    1    0    1    0    0
[7,]    1    0    1    1    0    0    1    1
[8,]    0    1    0    0    1    0    1    0
neighbours.mat
     [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,]    4    2    3    4    5    6    5    5
[2,]    2    1    2    4    5    6    4    4
[3,]    3    1    1    4    3    5    4    5
[4,]    3    2    1    3    1    3    2    3
[5,]    4    5    3    4    3    3    4    4
[6,]    5    6    5    4    3    1    4    6
[7,]    4    6    5    4    4    4    3    4
[8,]    4    2    4    5    4    6    5    6

That works: you can look at any cell in sim.grid, count the neighbours and then check it against the count in neighbours.mat and you should see the correct number. Remember that edges and corners wrap around.

Good. We can set up our original population and get a count of all the neighbours. What we need to do now is to use that neighbour count to generate a new matrix with the locations of the live cells in the next generation. There are a number of ways to do this, and you might think that the simplest would to just use a pair of nested for() loops like we did to count the cells. Let’s start with that. We’ll write a little function to apply the rules, and then run it through a set of loops.

#########function to apply rules

rules<-function(x) {

if (x==0 & num.neighbours==3) x<-1
if (x==1 & num.neighbours<2) x<-0
if (x==1 & num.neighbours>3) x<-0
x
}

This is (hopefully) self-evident: if the cell is dead (x==0) and the number of neighbouring live cells is 3 (num.neighbours==3) then a new cell is born: x<-1. If the cell is live (x==1) and has fewer than 2 (num.neighbours<2) or more than 3 (num.neighbours>3) neighbours then the cell dies and x<-0. We don’t need to specify the cases where a live cell remains alive (2 or 3 neighbours) because the cell doesn’t change in these cases.

Now all we have to do is to apply this function to each cell in our sim.grid matrix and we’ll have the population for our next generation.

#####Generate sim.grid for next generation

for (p in 1:grid.size){
  for (q in 1:grid.size){
    num.neighbours<-neighbours.mat[p,q]
    sim.grid[p,q]<-rules(sim.grid[p,q])
  }
}

We’re nearly there. Two things are left: first, we need to put the code which counts the neighbours and works out the new distribution of cells into a(nother) loop which will run once per generation, and secondly we want to plot the distribution of cells so that the user can see how it changes over time. Let’s do the plot first. What we want is a 2D graph representing the 2D matrix with the X- and Y- coordinates being the column and row numbers respectively and a plot symbol for each live cell in the matrix. There are lots of different options for making a plot of a matrix like this in R, one obvious one being the image() function. This will take a matrix and plot a graph with different colour levels representing the numbers in each cell of the matrix. image() might seem like an obvious candidate but it is not a great function for our purposes, however: the kind of plot produced, with cells being square-edged rectangles doesn’t look too great and more importantly it runs very slowly. One alterntaive would be to use the ggplot2 package which will draw similar plots quite easily - for ggplot2 enthusiasts this is done using the tile aesthetic - but this still has the problem of the square-edged rectangles representing each cell, which is fine for many purposes but not for this, and it would probably also run quite slowly. I haven’t tested it but ggplot2 is known for being optimised for flexibility and looks rather than speed, at least at the time of writing. What we’re going to do is to convert the matrix into a data frame with one variable for the X-coordinate, one for the Y and then a third for whether the cell is live or dead, and then use good old plot() to produce our figure. The tricky bit here is converting the matrix into XY coordinates, but help is at hand in the form of the reshape package. This has a handy function melt() which will do exactly what we want. I should mention here that both reshape and ggplot2 are written by the same person - Hadley Wickham of Rice University, who is one of the real standout people producing superb packages for R and making their work available for free. Thanks.

Here’s the code to draw our plot.

##Check for and load the reshape2 package
require(reshape2) 

## convert matrix into long data frame
plot.mat<-melt(sim.grid)

par(mar=c(1, 1, 4, 1))

plot(plot.mat$Var1[plot.mat$value==1],plot.mat$Var2[plot.mat$value==1],cex=50*1/grid.size,col="steelblue",pch=16,xlim=c(0.5,grid.size+0.5),ylim=c(0.5,grid.size+0.5),xaxs="i",yaxs="i",xaxt="n",yaxt="n",xlab="",ylab="",main=paste("Generation",i))

require() is a function which loads a package, just like library(), but we tend to use it to load packages inside functions because if the package is not installed it will give a warning which will make the problem clear. Once reshape2 is loaded we use melt() to generate our data frame. This will have three variables: Var1, the X-coordinates, Var2, the Y-coordinates and value which is the numbers that were at each point in the matrix. In our case these will be either zeros or ones. The par(mar) call changes the plot margins to make them thinner - note that in the final version we can put in a further par(mar=c(5, 4, 4, 2) + 0.1) at the end of the function to reset the margins to the default values. This will stop the user having to reset them herself or himself.

The massive plot() command is a bit harder to get through. We can quickly break it down to explain what’s going on.

plot(plot.mat$Var1[plot.mat$value==1],plot.mat$Var2[plot.mat$value==1] specifies which points should be plotted. What we’re doing by using the plot.mat$value==1 subscript for our X and Y variables is making sure that only the live cells get plotted.

cex=50*1/grid.size,col="steelblue",pch=16 is a set of arguments that determine the plot symbols, the latter two setting the colour and the actual symbol. cex=50*1/grid.size determines the size of the plot symbols and we are adjusting it by the size of the grid, so that larger grids gives us smaller plot symbols. How did I come up with 50*1/grid.size? Not, alas, from my tremendous mathematical intuition but by trial and error. I did it so you don’t have to.

xlim=c(0.5,grid.size+0.5),ylim=c(0.5,grid.size+0.5),xaxs="i",yaxs="i",xaxt="n",yaxt="n",xlab="",ylab="" is a set of arguments that get the axes how we want them. The xlim and ylim arguments set the axis limits and using xaxs and yaxs set to “i” means that the axes are scaled without any padding around the limits (look these up with ?par if necessary). The next four arguments suppress the axis plotting, so there are no tick marks or scales, and then the last two mean that there aren’t any axis labels.

Finally, main=paste("Generation",i) writes the generation number as the main plot title. Notice that we’re using the paste() function to put together the word “generation” and the number, which we’re getting from the counter in the loop that we’re going to have iterating each generation.

17.1 Our first version

OK, let’s put all of that together with a big fat loop to run each generation.


life<-function(grid.size=12,start=50,generations=50) {

#####Set up initial population

  init<-sample(c(rep.int(1,times=start),rep.int(0,times=(grid.size^2)-start)),size=grid.size^2,replace=FALSE)

  sim.grid<-matrix(data=init,nrow=grid.size)

#####Function to count neighbours

    neighbours<-function(R,C) {
      Rs<-c(R-1,R,R+1)
      Cs<-c(C-1,C,C+1)

      Rs<-ifelse(Rs==0,grid.size,Rs)    #what to do if it's on an edge
      Rs<-ifelse(Rs==grid.size+1,1,Rs)
      Cs<-ifelse(Cs==0,grid.size,Cs)
      Cs<-ifelse(Cs==grid.size+1,1,Cs)

#count the neighbours. -1 for the one in the middle

    count<-ifelse(sim.grid[R,C]==1,sum(sim.grid[Rs,Cs])-1,sum(sim.grid[Rs,Cs]))
  count
  }

#####Function to apply the rules of Life

  rules<-function(x) {

    if (x==0 & num.neighbours==3) x<-1
    if (x==1 & num.neighbours<2) x<-0
    if (x==1 & num.neighbours>3) x<-0
  x
  }

######Loop each generation

  for (i in 1:generations) {

######Calculate new matrix with number of neighbours

  neighbours.mat<-matrix(data=NA,nrow=grid.size,ncol=grid.size)

  for (p in 1:grid.size){
    for (q in 1:grid.size){
      neighbours.mat[p,q]<-neighbours(R=p,C=q)
    }
  }


#####Generate sim.grid for next generation

for (p in 1:grid.size){
  for (q in 1:grid.size){
    num.neighbours<-neighbours.mat[p,q]
    sim.grid[p,q]<-rules(sim.grid[p,q])
  }
}

#####Plot distribution of live cells

##Check for and load the reshape2 package
require(reshape2)

## convert matrix into long data frame
plot.mat<-melt(sim.grid)   

par(mar=c(1, 1, 4, 1))

plot(plot.mat$Var1[plot.mat$value==1],plot.mat$Var2[plot.mat$value==1],cex=50*1/grid.size,col="steelblue",pch=16,xlim=c(0.5,grid.size+0.5),ylim=c(0.5,grid.size+0.5),xaxs="i",yaxs="i",xaxt="n",yaxt="n",xlab="",ylab="",main=paste("Generation",i))

par(mar=c(5, 4, 4, 2) + 0.1)
}
}

If you enter this into R, best by pasting it into a script window and running it from there, you will be able to run the Game of Life. Try it, it works! There are some things that we can improve, though. If you’ve had a bit of a play with the function as it stands you’ve probably noticed quite a few problems with it. These are:

If the grid size is small, it runs too quickly to see what’s going on.
If the grid size is big, it can run very slowly. The definition of “big” and “small” here will depend on the machine you’re using but for this Apple MacBook anything under a grid size of about 15 runs too fast to see, and grid sizes greater than 100 get very slow.
If you have a relatively small starting population it will often go extinct and then you have to sit and stare at a blank plot until the simulation finishes running.
There are some configurations of cells which are stable (e.g four cells arranged in a square with no neighbours) and sometimes the population will end up with just some of these which you then stare at while it counts up to your number of generations.

Three of these problems, the fast speed on small grids and the questions of what to do when the population goes extinct or reaches a steady state, can be dealt with quite easily by adding a little to our existing function. For the problem of slow performance with large grids we need to think about optimising our code, which in the case of R means trying to replace those conceptually simple, easy to code but slooooooow loops with something a bit quicker. We’ll look at that once we’ve got the first two points sorted out.

To slow everything down on small grids we can introduce a pause into each loop. There is a function called Sys.sleep() which will put in a pause of a specified length, so that will do the trick. We want something that the user can turn on or off, so we’ll put in another argument for our function called slow: if this is FALSE then we won’t run Sys.sleep() but if it’s TRUE we will. Our function call therefore looks like this now:

life<-function(grid.size=12,start=50,generations=50,slow=FALSE) {
}

and just before the end of the big loop that iterates each generation we can put in this line of code:

##Introduce a 0.2 second pause for each iteration if slow=TRUE
if (slow==TRUE) Sys.sleep(0.2)

What about the problem of the population dying out? If this happens we want to stop the loop, which we can do with the break command. It would also be useful to show a message to let the user know that this has happened. If the population is extinct then the sum of all the values in the sim.grid matrix will be zero, and we can use this to tell the function what to do when everything’s dead using an if() function.

##If all dead break and show message  
if(sum(sim.grid)==0) {
    text(x=grid.size/2,y=grid.size/2, 
      "When you play the game of life,\n you win or you die.\n There is no middle ground",cex=1.5)
    break
}

We can put this just after our Sys.sleep() instruction, at the end of the loop, and each time the loop runs it will check if everything’s dead. If this is the case it will firstly write a message onto the plot using the text() function (note the use of the \n characters to introduce carriage returns), and then it will break the loop, finishing off the simulation.

What about the situation where the population isn’t extinct, but isn’t changing? How can we stop the function if this happens? There’s an easy way to detect this, because if the population isn’t changing then if we subtract our matrix for generation i-1 from our matrix for generation i and sum the result we will get zero. There are two problems with this, however. The first is that we have overwritten our matrix from population i-1, so we need to put something in at the start of the loop to make a copy of the matrix from the previous generation.

######Loop each generation

  for (i in 1:generations) {
    sim.grid.last<-sim.grid
}

The second problem is that there are other combinations of matrices that will give us zero when we sum the result of subtracting one from the other, because we can have negative values as well as positive ones and if there are as many -1 cells as 1 cells we’ll get zero when we don’t want to stop the simulation. This can be avoided by looking at the sum of the unsigned values when we subtract sim.grid.last from sim.grid, which can be obtained with the abs() function.

These issues sorted out, we can add another if() .... break instruction at after the one for when the population’s extinct. The keen of mind will have noted that “everything dead” will also give a zero value here, but if we put this after the check for no population it will only happen when the population is greater than zero.

######If steady state break and show message

if(sum(abs(sim.grid-sim.grid.last))==0)
    text(x=grid.size/2,y=grid.size/2, 
      "Unlike the universe,\n The Game of Life\n has reached a steady state",cex=1.5)
    break

Here’s our improved version:


life<-function(grid.size=12,start=50,generations=50,slow=FALSE) {


#####Set up initial population

  init<-sample(c(rep.int(1,times=start),rep.int(0,times=(grid.size^2)-start)),size=grid.size^2,replace=FALSE)

  sim.grid<-matrix(data=init,nrow=grid.size)

#####Function to count neighbours

    neighbours<-function(R,C) {
      Rs<-c(R-1,R,R+1)
      Cs<-c(C-1,C,C+1)

      Rs<-ifelse(Rs==0,grid.size,Rs)    #what to do if it's on an edge
      Rs<-ifelse(Rs==grid.size+1,1,Rs)
      Cs<-ifelse(Cs==0,grid.size,Cs)
      Cs<-ifelse(Cs==grid.size+1,1,Cs)

#count the neighbours. -1 for the one in the middle
    count<-ifelse(sim.grid[R,C]==1,sum(sim.grid[Rs,Cs])-1,sum(sim.grid[Rs,Cs]))  
  count
  }

#####Function to apply the rules of Life

  rules<-function(x) {

    if (x==0 & num.neighbours==3) x<-1
    if (x==1 & num.neighbours<2) x<-0
    if (x==1 & num.neighbours>3) x<-0
  x
  }

######Loop each generation

  for (i in 1:generations) {

      sim.grid.last<-sim.grid

######Calculate new matrix with number of neighbours

  neighbours.mat<-matrix(data=NA,nrow=grid.size,ncol=grid.size)

  for (p in 1:grid.size){
    for (q in 1:grid.size){
      neighbours.mat[p,q]<-neighbours(R=p,C=q)
    }
  }


#####Generate sim.grid for next generation

for (p in 1:grid.size){
  for (q in 1:grid.size){
    num.neighbours<-neighbours.mat[p,q]
    sim.grid[p,q]<-rules(sim.grid[p,q])
  }
}

#####Plot distribution of live cells

##Check for and load the reshape2 package
require(reshape2)

## convert matrix into long data frame
plot.mat<-melt(sim.grid)   

plot(plot.mat$Var1[plot.mat$value==1],plot.mat$Var2[plot.mat$value==1],cex=50*1/grid.size,col="steelblue",pch=16,xlim=c(0.5,grid.size+0.5),ylim=c(0.5,grid.size+0.5),xaxs="i",yaxs="i",xaxt="n",yaxt="n",xlab="",ylab="",main=paste("Generation",i))

##Introduce a 0.2 second pause for each iteration if slow=TRUE
if (slow==TRUE) Sys.sleep(0.2)


##If all dead break and show message  
if(sum(sim.grid)==0) {
    text(x=grid.size/2,y=grid.size/2, 
      "When you play the game of life,\n you win or you die.\n There is no middle ground",cex=1.5)
  break
}

######If steady state break and show message
if(sum(abs(sim.grid-sim.grid.last))==0) {
    text(x=grid.size/2,y=grid.size/2, 
      "Unlike the universe,\n The Game of Life\n has reached a steady state",cex=1.5)
    break
}

par(mar=c(5, 4, 4, 2) + 0.1)

}
}

17.2 Speeding it up

This new version of our function now has all the bells and whistles that the previous version lacked, featuring an option to slow it down when it’s too fast and some bits and pieces that stop the loop when nothing’s happening and inform the user with Humorous Messages, but we still need to look at the speed when we’re running the Game on a large grid. There are a number of approaches we can take to do this. Fistly, everything that’s in a loop will happen every time the loop runs, so if there are components of the code which are currently inside loops and could be moved outside, either to the start or the finish of the function, then we should do that. Three candidates are the require(reshape2) instruction which loads the reshape2 package: this can be moved to the beginning of the function, as can the par(mar=c(1,1,4,1)) instruction to change the plot parameters. The second par(mar=) instruction, which resets the plot margins, can also go outside the loop and be placed right at the end of the function.

Here’s a new version with those changes. I haven’t included most of the code because it’s the same as before. I’ve renamed the function to life2 so that we can compare its performance with life using system.time().


life2<-function(grid.size=12,start=50,generations=50,slow=FALSE) {

###Check for and load the reshape2 package
require(reshape2)

###Set plot margins to small
par(mar=c(1, 1, 4, 1))

...


#####Plot distribution of live cells

## convert matrix into long data frame
plot.mat<-melt(sim.grid)


plot(plot.mat$Var1[plot.mat$value==1],plot.mat$Var2[plot.mat$value==1],cex=50*1/grid.size,col="steelblue",pch=16,xlim=c(0.5,grid.size+0.5),ylim=c(0.5,grid.size+0.5),xaxs="i",yaxs="i",xaxt="n",yaxt="n",xlab="",ylab="",main=paste("Generation",i))

...

######If steady state break and show message
if(sum(abs(sim.grid-sim.grid.last))==0) {
    text(x=grid.size/2,y=grid.size/2, 
      "Unlike the universe,\n The Game of Life\n has reached a steady state",cex=1.5)
    break
}

}
##Reset margins
par(mar=c(5, 4, 4, 2) + 0.1)
}

How do they compare?

system.time(life(start=200,generations=20,grid.size=30,slow=FALSE))
   user  system elapsed 
  1.055   0.069   1.148 
system.time(life2(start=200,generations=20,grid.size=30,slow=FALSE))
   user  system elapsed 
  1.163   0.078   1.274

Hard to say: they’re still very close although we might see a difference if we run them both several times: here we’re using replicate() for this and then getting the total elapsed time for our 40 reps of each from the third row of the saved objects. NB if you try and run this yourself it might take a while.

life.test<-replicate(40,system.time(life(start=200,generations=10,grid.size=30,slow=FALSE)))
life2.test<-replicate(40,system.time(life2(start=200,generations=10,grid.size=30,slow=FALSE)))
summary(life.test[3,])
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  0.518   0.537   0.573   0.594   0.629   0.783 
summary(life2.test[3,])
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  0.500   0.522   0.533   0.545   0.555   0.697

Nope. No difference visible: it’s all eaten up in the stochastic noise of the simulations. Oh well.

It looks like we’re going to have to go after those loops. The function at the moment is lousy with loops, including loops within loops, and these will all be slowing things down. We won’t be able to get rid of the main loop which runs once per iteration, but how about those smaller nested loops that we use firstly to count the number of neighbours and then secondly to apply the rules? Can we replace those with something faster?

You will not be surprised to hear that the answer is “Yes. Yes we can.” The really easy one to get rid of is the nested loop that we use to work out which cells are born, stay alive or die on the basis of the number of neighbours that they have. Just to remind you, this piece of code looks like this:

#####Function to apply the rules of Life

  rules<-function(x) {

    if (x==0 & num.neighbours==3) x<-1
    if (x==1 & num.neighbours<2) x<-0
    if (x==1 & num.neighbours>3) x<-0
  x
  }

first the function to aply the rules and then later on, each time we iterate:

#####Generate sim.grid for next generation

for (p in 1:grid.size){
  for (q in 1:grid.size){
    num.neighbours<-neighbours.mat[p,q]
    sim.grid[p,q]<-rules(sim.grid[p,q])
  }
}

We can replace this whole doubley-loopy set of code with a much shorter, simpler and faster piece of code - 3 lines! by using R’s capacity for putting logical tests in its subscripts. This is what we can put in instead. There’s no need for a separate rules() function at all. All we do is make changes to our matrix on the basis of three logical tests based on the rules of life as follows. This not only shortens the function but also speeds it up.

sim.grid[sim.grid==0 & neighbours.mat==3]<-1
sim.grid[sim.grid==1 & neighbours.mat<2]<-0
sim.grid[sim.grid==1 & neighbours.mat>3]<-0

I’m not going to put the altered function in for reasons of brevity but you can download it from the module webpage if you like. Is it any faster?

life.test<-replicate(40,system.time(life(start=200,generations=10,grid.size=30,slow=FALSE)))
life3.test<-replicate(40,system.time(life3(start=200,generations=10,grid.size=30,slow=FALSE)))

We can run our little test once more and then look at the summaries of the elapsed times.

summary(life.test[3,])
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  0.484   0.507   0.523   0.525   0.539   0.582 
summary(life3.test[3,])
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  0.488   0.528   0.538   0.563   0.561   0.844

Looks like our new function is a fair bit faster. We can see how confident we should be in this difference with a t-test.

t.test(life.test[3,],life3.test[3,])

    Welch Two Sample t-test

data:  life.test[3, ] and life3.test[3, ]
t = -2.97, df = 45.7, p-value = 0.0047
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.064037 -0.012313
sample estimates:
mean of x mean of y 
  0.52513   0.56330

Not much question there. Our new version of life is about 10% faster than the previous version. This is still not a huge change, however. Can we do something about the set of loops we use to count the number of neighbours? Again, the answer is yes, with a very elegant solution which I first came across online here a blog written by Petr Keil. This relies on the fact that matrix operations in R are very fast, by contrast with loops. Instead of iterating through every cell in the matrix using a set of nested loops, we can count the neighbours by making eight new matrices, each shifted by one cell in one of the eight locations corresponding to one of the eight neighbouring cells, and summing them. Think of this as making a stack of new matrices, each one moved by one cell in one of the 8 directions: if select a cell at the top of the stack and drill through it, all the way through the whole pile of matrices, and add the number of live cells you go through, that number will correspond to the number of neighbours for the corresponding cell in the original matrix.

Because we’re working on a toroidal world, we can do these shifts by taking the appropriate row or column from one side and adding it on to the other side of the matrix. As an example, if we want to make a matrix shifted to the right (I’ll follow the original article and call this shifting the matrix East) we can do this by taking the last column from the right hand side of the matrix and moving it to the left hand side using the cbind() function. As an example, here’s our matrix:

sim.grid
     [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,]    0    0    0    1    1    1    1    1
[2,]    1    0    0    1    1    0    1    1
[3,]    0    0    0    0    1    0    0    0
[4,]    0    0    0    0    1    0    1    1
[5,]    1    0    1    0    0    0    0    1
[6,]    1    1    1    1    0    1    0    0
[7,]    1    0    1    1    0    0    1    1
[8,]    0    1    0    0    1    0    1    0

The matrix is 8 columns across so we can move it “East” by taking the 8th column and adding it as the first column.

sim.gridE <- cbind(sim.grid[,8],sim.grid[,-8])
sim.gridE
     [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,]    1    0    0    0    1    1    1    1
[2,]    1    1    0    0    1    1    0    1
[3,]    0    0    0    0    0    1    0    0
[4,]    1    0    0    0    0    1    0    1
[5,]    1    1    0    1    0    0    0    0
[6,]    0    1    1    1    1    0    1    0
[7,]    1    1    0    1    1    0    0    1
[8,]    0    0    1    0    0    1    0    1

We can replace the code for the neighbours() function and for the nested loop that iterates through all the cells in the matrix with these lines of code.

###Make a stack of new matrices shifted by one in each direction

allW <- cbind(sim.grid[,-1],sim.grid[,1])
allN <- rbind(sim.grid[-1,],sim.grid[1,])
allE <- cbind(sim.grid[,grid.size],sim.grid[,-grid.size])
allS <- rbind(sim.grid[grid.size,],sim.grid[-grid.size,])
allNW<-rbind(allW[-1,],allW[1,])
allNE<-rbind(allE[-1,],allE[1,])
allSW<-rbind(allW[grid.size,],allW[-grid.size,])
allSE<-rbind(allE[grid.size,],allE[-grid.size,])

###Get the number of neighbours by summing the new matrices
neighbours.mat <- allW + allNW + allN + allNE + allE + allSE + allS + allSW

So now we can produce a final, hopefully super-speedy life4() function with all of the loops except one replaced with faster and simpler code. Here it is.


life4<-function(grid.size=12,start=50,generations=50,slow=FALSE) {

require(reshape2) ###Check for and load the reshape2 package

par(mar=c(1, 1, 4, 1)) ###Set plot margins to small

#####Set up initial population

  init<-sample(c(rep.int(1,times=start),rep.int(0,times=(grid.size^2)-start)),size=grid.size^2,replace=FALSE)

  sim.grid<-matrix(data=init,nrow=grid.size)

######Loop each generation

  for (i in 1:generations) {

      sim.grid.last<-sim.grid

###Make a stack of new matrices shifted by one in each direction

allW <- cbind(sim.grid[,-1],sim.grid[,1])
allN <- rbind(sim.grid[-1,],sim.grid[1,])
allE <- cbind(sim.grid[,grid.size],sim.grid[,-grid.size])
allS <- rbind(sim.grid[grid.size,],sim.grid[-grid.size,])
allNW<-rbind(allW[-1,],allW[1,])
allNE<-rbind(allE[-1,],allE[1,])
allSW<-rbind(allW[grid.size,],allW[-grid.size,])
allSE<-rbind(allE[grid.size,],allE[-grid.size,])

###Get the number of neighbours by summing the new matrices
neighbours.mat <- allW + allNW + allN + allNE + allE + allSE + allS + allSW


#####Generate sim.grid for next generation

sim.grid[sim.grid==0 & neighbours.mat==3]<-1
sim.grid[sim.grid==1 & neighbours.mat<2]<-0
sim.grid[sim.grid==1 & neighbours.mat>3]<-0

#####Plot distribution of live cells

plot.mat<-melt(sim.grid)   ## convert matrix into long data frame

plot(plot.mat$Var1[plot.mat$value==1],plot.mat$Var2[plot.mat$value==1],cex=50*1/grid.size,col="steelblue",pch=16,xlim=c(0.5,grid.size+0.5),ylim=c(0.5,grid.size+0.5),xaxs="i",yaxs="i",xaxt="n",yaxt="n",xlab="",ylab="",main=paste("Generation",i))

##Introduce a 0.2 second pause for each iteration if slow=TRUE
if (slow==TRUE) Sys.sleep(0.2)


##If all dead break and show message  
if(sum(sim.grid)==0) {
    text(x=grid.size/2,y=grid.size/2, 
      "When you play the game of life,\n you win or you die.\n There is no middle ground",cex=1.5)
  break
}

######If steady state break and show message
if(sum(abs(sim.grid-sim.grid.last))==0) {
    text(x=grid.size/2,y=grid.size/2, 
      "Unlike the universe,\n The Game of Life\n has reached a steady state",cex=1.5)
    break
}

}
par(mar=c(5, 4, 4, 2) + 0.1)  ##Reset margins
}

How much faster is it now?

life.test<-replicate(40,system.time(life(start=200,generations=10,grid.size=30,slow=FALSE)))
life4.test<-replicate(40,system.time(life4(start=200,generations=10,grid.size=30,slow=FALSE)))

We can run our little test once more and then look at the summaries of the elapsed times.

summary(life.test[3,])
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  0.488   0.521   0.540   0.551   0.558   0.798 
summary(life4.test[3,])
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  0.306   0.334   0.346   0.352   0.370   0.418

Don’t think we need a t-test for this. Our new function is much, much faster now, with almost all of that speed improvement coming from replacing the neighbour-counting loops with the extremely fast matrix operations. On my MacBook Pro this function will now run a Game of Life on a 250x250 grid (that’s 62,500 individual cells) at a reasonable and watchable speed.

Xie, Yihui. 2015. Dynamic Documents with R and Knitr. 2nd ed. Boca Raton, Florida: Chapman; Hall/CRC. http://yihui.name/knitr/.

———. 2016. Bookdown: Authoring Books and Technical Documents with R Markdown. Boca Raton, Florida: Chapman; Hall/CRC. https://github.com/rstudio/bookdown.