Chapter 12 Working with matrices and data frames
Let’s say that you have a matrix of data, and you want to know the mean of each row, or that you have a data frame with several different numeric variables and you want to know the slope of a linear regression relating variable 1 to variable 2 for each of 5 levels of a factor. You are in luck: R has a whole suite of functions which allow you to apply other functions across vectors and matrices. Most of these functions are based on the apply() function, although the relationship can be hard to discern in some cases, and they allow complicated operations to be carried out quickly and with minimal amounts of code. Some of these processes nowadays can be done easily using the package dplyr, which we will met in a couple of chapters. Even if you’re a committed dplyrist, however, you’ll need to know about these functions if for no other reason than to understand other people’s code. When there’s an easy dplyr alternative we’ll mention it: if you don’t know dplyr yet this will be a bit obscure but it will hopefully be useful for future reference.
The chief difficulty with these functions is that there is a baffling range of them, and a lot of people (including your author) get confused about which particular function to use. In an attempt to reduce the confusion, here’s a quick lookup table which should help you navigate through the maze.
| I want to | Function to use |
|---|---|
| Do a calculation or apply a function on every row or column of a matrix, or a selection of them | apply() |
| Do a calculation or carry out a function on every member of a list and get a vector or matrix back | sapply() |
| Do a calculation or carry out a function on every member of a list and get a list back | lapply() |
| Split a vector by the levels of one or more factors and do a calculation or carry out a function according to the levels of the factor(s) | tapply() |
| Split a data frame according to the levels of a factor and apply a function to each piece of data frame | by() |
| Split a data frame according to the levels of a factor and apply a function to each variable in each piece of data frame | aggregate() |
| Carry out a function multiple times to produce a list or matrix | replicate() |
12.1 Rows or columns of matrices: apply()
This function carries out operations on rows or columns of matrices. The arguments it takes are firstly the name of the matrix, secondly an argument called “margin” which can be 1 (meaning carry out the function for each row), 2 (carry out the function for each column) or c(1,2) which will carry out the function on both rows and columns. Here’s a matrix which we’d like the row totals for.
mat1 <- matrix(rnorm(1000), nrow = 100)This sets up a matrix called mat1 with 100 rows, using 1000 randomly generated numbers drawn from a standard normal distribution. To calculate the mean of each row= of this matrix you can use this code:
rowmeans <- apply(mat1, 1, mean)Just to check it’s working, here are the first 10 values of of the new vector:
rowmeans[1:10]
[1] -0.013224 -0.031643 -0.706078 -0.032552 -0.646624 -0.385629 0.816833
[8] 0.025789 0.462057 -0.281147We could have done exactly the same calculation using a for() loop (see next chapter) but doing it this way is shorter and you don’t need a separate line of code to set up a vector to put your output in.
The example above used the mean() function, but you can use any function. Want the smallest value for each column?
colmins <- apply(mat1, 2, min)
colmins[1:10]
[1] -3.3117 -1.9625 -2.0277 -3.2672 -2.2171 -3.6105 -2.1295 -2.8706 -2.2498
[10] -2.9198You can use functions you’ve written yourself as well. Let’s say you want to calculate the coefficient of variation (the standard deviation divided byu the mean) for each row. First we need to specify our function.
cv_calc <- function(x) {
sd(x) / mean(x)
}Now we can use it in the apply() call.
mat1_cv<-apply(mat1,2,cv_calc)
mat1_cv[1:5]
[1] -5.6239 -18.0083 8.1097 6.7453 -20.465212.1.1 Using a nameless function in apply()
If you have a specific operation you want to carry out, like the coefficient of variation calculation above, you don’t have to write a separate function. If you won’t need the function anywhere else in your code you can put it directly in the apply() function call without giving it a name: what is called an anonymous or nameless function. Here’s how to do this for our coefficient of variation calculation.
mat1_cv <- apply(mat1, 1,
function(x) sd(x) / mean(x))
mat1_cv[1:5]
[1] -58.1589 -29.9901 -1.6578 -34.3475 -2.2421Here instead of just giving the name of a function we want to use we’ve defined a new function. It doesn’t need a name because it’s only being used within the apply() function call. Our un-named function has only one argument, x, and apply() will feed the data for each row (in this case) into that function as the x argument. In the section after the function() command we have the code which will be executed for our un-named function, and you can see that it’s taking the x argument from the function, calculating the standard deviation and then dividing it by the mean. One thing to remind you of is that we don’t need to put these instructions inside a set of braces because there’s only one line of code.
As of R 4.1, you can use a different syntax to generate an anonymous function by replacing function with a backslash \.
mat1_cv <- apply(mat1, 1,
\(x) sd(x) / mean(x))
mat1_cv[1:5]
[1] -58.1589 -29.9901 -1.6578 -34.3475 -2.242112.2 Operations on lists and data frames: sapply() and lapply()
These both apply an operation to each member of a list. Just to remind you, lists are objects which is themselves groups of named objects. The most common sort of list that you’re likely to encounter is a data frame, which of course contains a set of variables that can be numeric, logical or character data.
The difference between the two functions is that lapply() returns a list of results (remember L for List), whereas sapply() will try to produce the results as the simplest data object possible (remember S for Simple), which will usually be a vector or a matrix. Here’s an example: we’ll start with a set of made up data.
mydata <-
data.frame(matrix(rnorm(24), ncol = 3,
dimnames = list(
NULL,
c("Low.dose", "Medium.dose", "High.dose"))
))This makes a matrix with three columns filled with random random numbers, with no row names (the NULL entry in the dimnames argument) but the columns named “Low.dose,” “Medium.dose” and “High.dose.” This matrix is then comverted to a data frame using the data.frame() function.
sapply(mydata, mean)
Low.dose Medium.dose High.dose
-0.2920653 -0.6237200 0.0078242 sapply() gives us a vector containing the means of the three variables in the data frame. Remember the data frame is itself a list and each variable is an item in the list.
lapply(mydata, mean)
$Low.dose
[1] -0.29207
$Medium.dose
[1] -0.62372
$High.dose
[1] 0.0078242lapply() gives us a list, rather than a vector.
One thing to remember when using these functions is that you don’t have to apply them to the whole list: you can use subscripts to specify particular variables within your list. As an example let’s go back to the data on pollution from the World Bank that we used in the chapter on dplyr Let’s load the data frame into R. We’ll make the Region and Income_group variables into factors.
pollution <- read.csv("https://raw.githubusercontent.com/rjknell/Introductory_R_3rd_Edition/master/Data/CO2_PM25.csv")
pollution$Region <- as.factor(pollution$Region)
pollution$Income_group <- as.factor(pollution$Income_group)
str(pollution)
'data.frame': 186 obs. of 9 variables:
$ Country_Name : chr "Afghanistan" "Angola" "Albania" "Andorra" ...
$ Country_Code : chr "AFG" "AGO" "ALB" "AND" ...
$ Region : Factor w/ 7 levels "East Asia & Pacific",..: 6 7 2 2 4 3 2 3 1 2 ...
$ Income_group : Factor w/ 4 levels "High income",..: 2 3 4 1 1 4 4 1 1 1 ...
$ Population : int 33370794 26941779 2889104 79213 9214175 42669500 2912403 92562 23475686 8546356 ...
$ GNP_per_Cap : int 630 5010 4540 NA 44330 12350 4140 12730 65150 50370 ...
$ Population_growth: num 3.356 3.497 -0.207 -1.951 0.177 ...
$ CO2 : num 0.294 1.29 1.979 5.833 22.94 ...
$ PM25 : num 59 33 18.9 10.8 38 ...If you try to use sapply() to calculate the mean of each variable you get an error because the first four variables are either character data or factors. It still calculates the rest of the means, but it returns a warning and NA for the character variables.
sapply(pollution, mean)
Country_Name Country_Code Region Income_group
NA NA NA NA
Population GNP_per_Cap Population_growth CO2
3.8749e+07 NA 1.3668e+00 4.3225e+00
PM25
2.6525e+01 It also returns NA for the GNP-per-Cap (Gross National Product per capita) variable. This is because there is at least one NA value in the variable and mean() will return NA if at least one value is NA, unless you tell it not to.
What we can do to fix the warnings etc. we get for the character variables is to use a subscript in the sapply() call to specify that we only want the means of the numeric variables, which are the fifth to ninth inclusive in the data frame.
sapply(pollution[5:9],mean)
Population GNP_per_Cap Population_growth CO2
3.8749e+07 NA 1.3668e+00 4.3225e+00
PM25
2.6525e+01 All good except for the NA for GNP_per_Cap. If we need to we can fix this by using an anonymous function for mean() and adding the argument na.rm = TRUE which means it will just remove the NA values and then calculate the mean.
sapply(pollution[5:9], function(x) mean(x, na.rm = TRUE))
Population GNP_per_Cap Population_growth CO2
3.8749e+07 1.3343e+04 1.3668e+00 4.3225e+00
PM25
2.6525e+01 That now returns the mean values for all of the numeric variables. Note that
sapply(pollution[5:9], \(x) mean(x, na.rm = TRUE))with the \ shorthand for function would do exactly the same thing.
12.3 Functions for summarising data by factor levels: tapply(), aggregate() & by()
12.3.1 tapply()
The help file for tapply() is particularly obscure: the description reads “Apply a function to each cell of a ragged array, that is to each (non-empty) group of values given by a unique combination of the levels of certain factors”. Translating that into something approaching English, what the function does is to take a vector of data, divide it up according to the levels of one or more factors and then apply a function to the parts of the vector that apply to each factor level or combination. Looking back to our pollution data, we can use tapply() to calculate summary statistics for each factor level of Income_group or Region for any of the numeric variables in the data frame. Let’s start with CO2 production for the different income groups.
tapply(pollution$CO2, pollution$Income_group, mean)
High income Low income Lower middle income Upper middle income
9.46772 0.31712 1.21814 4.05665 12.3.1.1 tapply() with more than one factor
tapply() will work with more than one grouping factor, and when this is done it will apply the function specified to each combination of factor levels. To do this we need to supply tapply() with a list of the factors we would like our variable to be grouped by. Let’s say we need to calculate the standard deviation for CO2 production in our pollution dataset, but we’d like to break this down by both Income_group and Region. Our code would look like this.
tapply(pollution$CO2, list(pollution$Region, pollution$Income_group), sd)
High income Low income Lower middle income
East Asia & Pacific 5.2938 NA 1.81840
Europe & Central Asia 3.1001 NA 1.69568
Latin America & Caribbean 11.3474 NA 0.49198
Middle East & North Africa 7.9827 0.5384925 0.77936
North America 4.0927 NA NA
South Asia NA 0.0031939 0.55765
Sub-Saharan Africa NA 0.1306384 0.33626
Upper middle income
East Asia & Pacific 3.1032
Europe & Central Asia 3.9459
Latin America & Caribbean 1.2676
Middle East & North Africa 2.5660
North America NA
South Asia 1.5437
Sub-Saharan Africa 2.574012.3.1.2 tapply() or dplyr()?
tapply() is an example of an apply() family function that can easily be emulated using dplyr(). As an example, to calculate the mean CO2 production by income group, as we did in the first example, we can use the group_by() and summarise() verbs from dplyr like this.
library(dplyr)
pollution |> group_by(Income_group) |> summarise(meanCO2 = mean(CO2))
# A tibble: 4 × 2
Income_group meanCO2
<fct> <dbl>
1 High income 9.47
2 Low income 0.317
3 Lower middle income 1.22
4 Upper middle income 4.06 Which of these you use is your choice. The dplyr() approach benefits from the easily read pipeline rather than the rather more obscure code for tapply(). dplyr() also makes it much easier to produce multiple oiutputs when you summarise your data. If you wanted to know sample size, mean and variance for CO2 production for each level of Income_group you’d either need to run tapply() three times, or write a function to do it, either with a named function or an anonymous one.
summary_stats <- function(x) {
output <- numeric(length = 3)
names(output) <- c("N", "Mean", "Variance")
output[1] <- length(x)
output[2] <- mean(x)
output[3] <- var(x)
output
}
tapply(pollution$CO2, pollution$Income_group, summary_stats)
$`High income`
N Mean Variance
54.0000 9.4677 44.2938
$`Low income`
N Mean Variance
30.00000 0.31712 0.16340
$`Lower middle income`
N Mean Variance
46.0000 1.2181 1.5964
$`Upper middle income`
N Mean Variance
56.0000 4.0567 8.9214 Doing this works, but it returns a difficult to manage array with the data. Using the dplyr() approach is a lot simpler.
pollution |>
group_by(Income_group) |>
summarise(N = n(),
mean = mean(CO2),
variance = var(CO2))
# A tibble: 4 × 4
Income_group N mean variance
<fct> <int> <dbl> <dbl>
1 High income 54 9.47 44.3
2 Low income 30 0.317 0.163
3 Lower middle income 46 1.22 1.60
4 Upper middle income 56 4.06 8.92 This is much more efficient and gives us a tibble(), the tidyverse version of a data frame which in this context at least is a lot easier to read and work with than the array we got previously.
12.3.2 by()
by() is closely related to tapply(), but while tapply() works on a vector, by() works on a data frame. It will take a data frame, split it according to a factor and then apply a function to the bits of the whole data frame that correspond to each factor level. The syntax follows the same layout as the previous functions: the first argument is the thing to be divided and analysed, the second is the index factor to split it by and the third argument is the function to apply. Going back to our pollution data, if we wanted to calculate the means for each of the five numeric variables for each income group we could use by() as follows.
by(pollution[5:9],pollution$Income_group,colMeans)
pollution$Income_group: High income
Population GNP_per_Cap Population_growth CO2
2.1209e+07 NA 7.8635e-01 9.4677e+00
PM25
1.7677e+01
------------------------------------------------------------
pollution$Income_group: Low income
Population GNP_per_Cap Population_growth CO2
2.1135e+07 NA 2.2790e+00 3.1712e-01
PM25
3.7421e+01
------------------------------------------------------------
pollution$Income_group: Lower middle income
Population GNP_per_Cap Population_growth CO2
6.1999e+07 NA 1.7619e+00 1.2181e+00
PM25
3.2298e+01
------------------------------------------------------------
pollution$Income_group: Upper middle income
Population GNP_per_Cap Population_growth CO2
4.5999e+07 7.3870e+03 1.1132e+00 4.0567e+00
PM25
2.4477e+01 Two things to notice are first that we need to tell R only to use the fifth to ninth variables in the data frame so that we’re not trying to calculate a mean of a factor in the same way as we did with sapply(), and secondly that we’re using the colMeans() function, which you might not have seen before. colMeans() does what it says on the tin and calculates the means of each of a group of columns.
by() will return either an array or a list, whichever is simpler. In this case it returns a list, with each factor level for Income_group being an item in the list. Sometimes this is not what you want for your output, but it also means that you can use functions with by() that produce complex output that could not be saved as a matrix or a data frame. As an example, maybe you want to carry out a linear regression to relate CO2 production to wealth (in this case the GNP_per_Cap variable), but you want a separate regression for each income group. You can add an un-named function into by() to do this.
CO2_regs <-
by(pollution, pollution$Income_group,
function(x) lm(x$CO2 ~ x$GNP_per_Cap))This will produce a list called CO2_regs. Each item in the list is an object containing the output from the linear regression of log brain mass on log body mass for that particular family. You can access the regression for a chosen family by referring to it with the list name$object name syntax that you are hopefully familiar with now, so to see the estimated coefficients — the intercept and the slope — for the High income group you can use this.
coef(CO2_regs$`High income`)
(Intercept) x$GNP_per_Cap
7.6041e+00 5.4042e-05 The sapply() and lapply() functions that we’ve already seen will work on these lists much as they will on any other list, so if you want the coefficients for all the families you can use one of these functions. sapply() will give us a useful matrix of all the intercepts and slopes.
sapply(CO2_regs,coef)
High income Low income Lower middle income Upper middle income
(Intercept) 7.6041e+00 -0.10829011 -0.21135698 0.30619547
x$GNP_per_Cap 5.4042e-05 0.00046226 0.00059659 0.00050771Can we replicate this with dplyr? Yes we can, sort of. We can’t easily output a list with each item being a separate fitted lm() object, so we don’t have the huge amount of flexibility that brings. We can, however, extract the coefficients within the summarise() function call using the coef() function. Once again you might find the dplyr pipeline syntax clearer and easier. You can see that in this case we have to add an extra variable using mutate() to tell us which values are the slopes and which the intercepts.
pollution |>
group_by(Income_group) |>
summarise(estimate = coef(lm(CO2 ~ GNP_per_Cap))) |>
mutate (coefficient = c("Intercept", "Slope"), .before = "estimate")
# A tibble: 8 × 3
# Groups: Income_group [4]
Income_group coefficient estimate
<fct> <chr> <dbl>
1 High income Intercept 7.60
2 High income Slope 0.0000540
3 Low income Intercept -0.108
4 Low income Slope 0.000462
5 Lower middle income Intercept -0.211
6 Lower middle income Slope 0.000597
7 Upper middle income Intercept 0.306
8 Upper middle income Slope 0.000508 12.3.3 aggregate()
This summarises a data frame on the basis of one or more named grouping variables and a function. It works a lot like by() but it outputs a data frame rather than a list, hence the name: the results are aggregated into a data frame. The specified function is applied to each variable in turn rather than to the whole data frame. One big difference in the way you use it is that the grouping variable or variables have to be specified as a list. As an example, let’s obtain the mean CO2 production and PM2.5 exposure for each level of Income_group.
aggregate(pollution[8:9],list(Income=pollution$Income_group),mean)
Income CO2 PM25
1 High income 9.46772 17.677
2 Low income 0.31712 37.421
3 Lower middle income 1.21814 32.298
4 Upper middle income 4.05665 24.477Once again we’ve specified the numeric variables in the data frame so that we aren’t trying to calculate means on a factor. As mentioned before, the grouping variable or variables for aggregate must be given as a list, and in this case we’re also specifiying a name for the grouping variable.
12.4 repeating an expression: replicate()
replicate() is a function which allows output from particular expressions to be replicated. The first argument is n, the number of replicates to produce, and the second is the expression which tells R what should be replicated. This can be useful if you want to generate sets of random numbers, but it is also a good function to use when calculating statistics using randomisation techniques such as bootstrapping.
If you aren’t familiar with bootstrapping, it’s a nonparametric method for estimating statistics based on repeatedly sampling from the data sample that we have. We take the data and repeatedly sample with replacement from it, generating new data sets that are made from values from the original one. As an example, if we had a vector called X1 with the values 6,2,3,5,5,9 and 8 then we can use the sample() function to generate new datasets of the same length. sample() will randomly pick numbers from a vector and use them to produce a new vector. The size argument tells sample() how many numbers to pick for the new object and setting the replace argument to TRUE means that we once a number has been picked it remains available to be picked again, so any particular value can appear more than once in our new datasets.
X1<-c(6,2,3,5,5,9,8)
sample(X1,size=7,replace=TRUE)
[1] 5 9 9 8 9 5 5
sample(X1,size=7,replace=TRUE)
[1] 3 6 5 5 2 5 5
sample(X1,size=7,replace=TRUE)
[1] 6 3 9 8 3 5 3If we repeat this sampling exercise many times (typically 100 or 1000) then we can calculate the mean of each of our bootstrap replicates, and the distribution of these means can be used to estimate things like the 95% confidence intervals of the mean of the original data set. The easiest way to calculate lots of bootstrap replicates is to use replicate. Just to show you what the output looks like here is what you get if you use replicate() to generate 8 bootstrap replicates.
replicate(8, sample(X1, size = 7, replace = TRUE))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 3 5 5 8 2 3 6 2
[2,] 6 6 5 8 2 5 8 8
[3,] 6 3 5 9 2 6 6 5
[4,] 8 9 5 2 3 8 6 5
[5,] 8 5 9 5 8 2 8 3
[6,] 2 5 3 2 5 9 9 5
[7,] 5 6 5 5 3 6 5 5We don’t want 8 replicates though, we want lots - a thousand will do.
bootstraps <- replicate(1000, sample(X1, size = 7, replace = TRUE))replicate() will generate a matrix with 1000 columns, each a separate sample with replication from the original dataset. We want the means of each column, so we can use apply() to calculate these.
bootstrap.means <- apply(bootstraps, 2, mean)Just to remind you, the first argument for apply is the object to be used, the second indicates whether the function being applied should be used on the rows (1) or, as in this case, the columns (2), and the third specifies the function. This will return a vector called “bootstrap means” with 1000 numbers in it, each of which is the mean of one of our sampled sets of data. Let’s have a look at the frequency distribution of the means of our bootstrap replicates.
hist(bootstrap.means,col="grey",xlab="Mean",main="")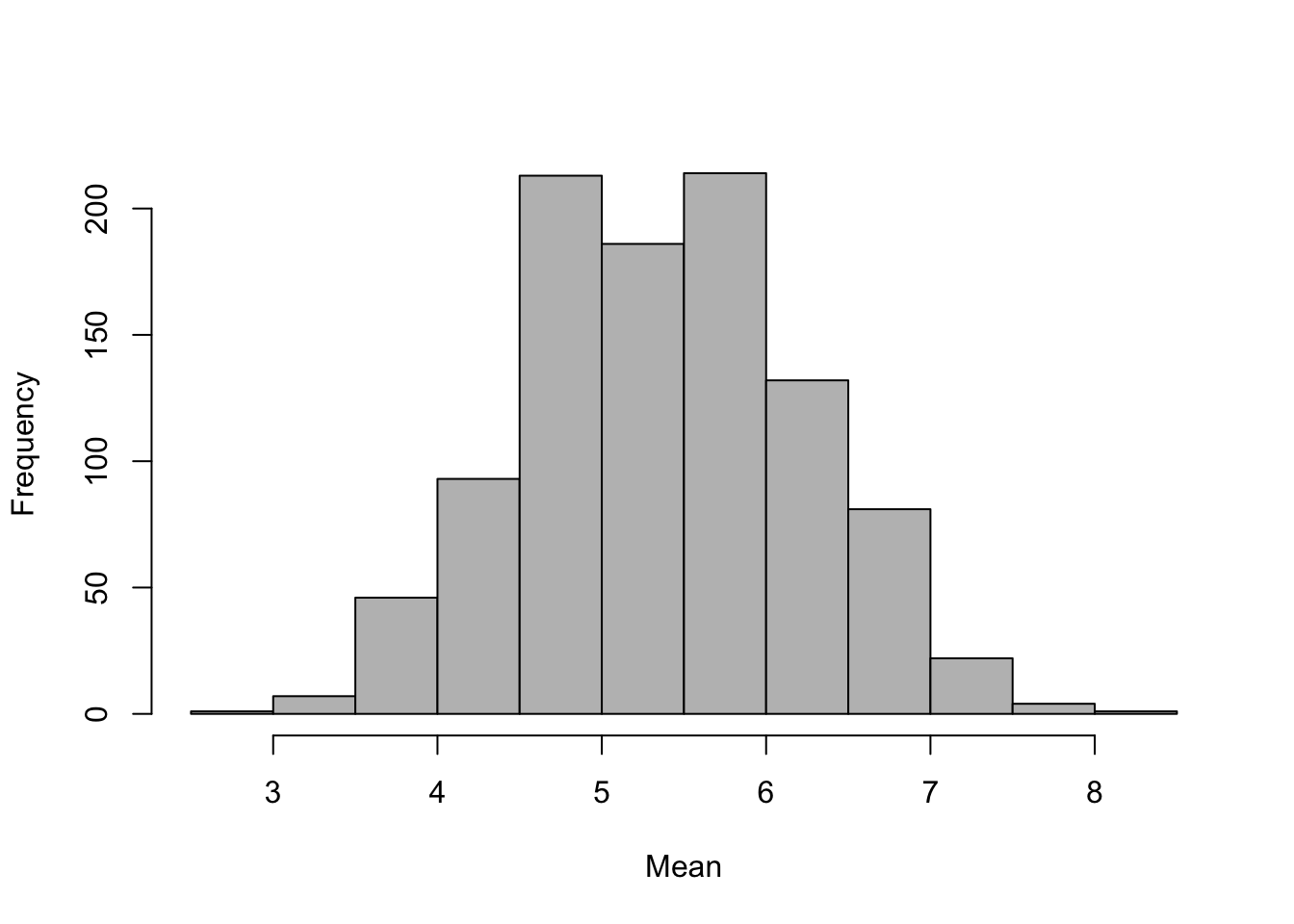
Figure 12.1: Frequency distribution of 1000 bootstrap means
We can use our 1000 means from our bootstrap replicates to estimate the 95% confidence limits for the mean - these are simply the 2.5% and 97.5% quantiles of our vector of means, which we can find using the quantile() function.
output<-c(quantile(bootstrap.means,0.025),quantile(bootstrap.means,0.975))
output
2.5% 97.5%
3.7143 7.1429 Let’s put these lines of code together to make a function.
boot.conf<-function(X1,conf=95) {
bootstraps <- replicate(1000,sample(X1,size=length(X1),replace=TRUE))
bootstrap.means<-apply(bootstraps,2,mean)
output<-c(quantile(bootstrap.means,(100-conf)/200),quantile(bootstrap.means,1-(100-conf)/200))
output
}To convert this into a function I’ve replaced the size=7 argument from the original first line with size=length(X1), which means that we can use a vector of any length, and I’ve added the same conf argument that we have in our parametric function so that the user can specify which confidence intervals are required. This has meant that I’ve replaced the 0.025 and 0.975 arguments from the quantile() functions in the second line with a slightly more complicated term which will calculate the appropriate numbers from conf. Let’s see if it works.
boot.conf(X1,conf=95)
2.5% 97.5%
3.7143 7.1464 How do these compare with the parametric confidence limits? We can use our meanci() function from the previous chapter to calculate these.
meanci(X1, conf=95)
Lower.CI Upper.CI
3.1099 7.7473 The bootstrap confidence intervals are a little narrower than the conventionally calculated ones.
As a final note, the bootstrap calculations above are a fine example of code that can be made more readable by using a pipeline: we’ll use this as an example in the next chapter.
12.5 See also…
In addition to these functions there are quite a few others which are useful for doing clever things with matrices and data frames in R. It’s probably a bit much to go into detail about them here but several of them at least need mentioning so that you’re aware of them.
12.5.1 t()
Transposes a matrix or a dataframe - in other words it swaps the rows for columns and vice-versa.
#t(whale.means)12.5.2 merge()
Merges two data frames together. Here’s an example using the pollution data. We want a new data frame with the means and standard deviations for CO2 production and PM2.5 exposure. We’ll start by using aggregate to generate separate data frames with the means and the standard deviations.
pollution_means <- aggregate(pollution[8:9],list(Income=pollution$Income_group),mean)
pollution_sds <- aggregate(pollution[8:9],list(Income=pollution$Income_group),sd)
pollution_means
Income CO2 PM25
1 High income 9.46772 17.677
2 Low income 0.31712 37.421
3 Lower middle income 1.21814 32.298
4 Upper middle income 4.05665 24.477
pollution_sds
Income CO2 PM25
1 High income 6.65536 13.571
2 Low income 0.40423 16.622
3 Lower middle income 1.26347 17.026
4 Upper middle income 2.98688 10.918Both the means and the standard deviations are calculated and recorded in data frames with three variables, in both cases with the same names. Before we merge these data frames we need to rename our mean and sd variables.
names(pollution_means) <- c("Income_group", "CO2_mean", "PM25_mean")
names(pollution_sds) <- c("Income_group", "CO2_sd", "PM25_sd")Now we can use merge() to join them together. merge() will look for a common variable in the two data frames to base the merge on, and in this case the common variable is Income_group.
pollution_summary<-merge(pollution_means, pollution_sds)
pollution_summary
Income_group CO2_mean PM25_mean CO2_sd PM25_sd
1 High income 9.46772 17.677 6.65536 13.571
2 Low income 0.31712 37.421 0.40423 16.622
3 Lower middle income 1.21814 32.298 1.26347 17.026
4 Upper middle income 4.05665 24.477 2.98688 10.918If the two data frames have a common variable which has a different name you can tell merge() which ones to use with the by.x= and by.y= arguments. Let’s rename the columns in pollution_sds again, and this time we’ll call Income)_group just Income.
names(pollution_sds)<-c("Income","CO2_sd","PM25_sd")
pollution_summary <-
merge(pollution_means, pollution_sds, by.x = "Income_group", by.y = "Income")
pollution_summary
Income_group CO2_mean PM25_mean CO2_sd PM25_sd
1 High income 9.46772 17.677 6.65536 13.571
2 Low income 0.31712 37.421 0.40423 16.622
3 Lower middle income 1.21814 32.298 1.26347 17.026
4 Upper middle income 4.05665 24.477 2.98688 10.91812.5.3 colMeans(), rowMeans(), colSums(), rowSums()
We’ve already met colMeans() in the section on by() but it’s worth mentioning all of these again. If you want to obtain the means or the sums of every row or column in a matrix these specific functions are also available and will do the job very quickly for you.
12.6 Exercises
Load and attach the haemocyte data which we previously used in chapter 9.
Use
apply()to calculate the overall mean for Weight and for Count. Remember that you’re dealing with a data frame not a matrix and that the first variable (Species) is not numeric so you’ll have to tellapply()to only use the second and third variables in the data frame.Use
tapply()to calculate the mean Weight and Count for both species. This will take two separate instructions.Now use
aggregate()to calculate the mean Weight and Count for both species. You should be able to do this wiht just one instruction.Use
by()to return the intercept and slope for a regression of Count on Weight for the two species analysed separately. This one is a little tricky - you’ll have to use the “write your own little function into the place for the function” trick. Remember thatby()splits your data frame into new data frames for analysis so you’ll need to refer to the variables in the regression as being part of the new data frame (e.g. function(x) ….x$Count rather than function(x) …Count). You can get the intercept and slope from a model by getting the coefficients.Use
replicate()to generate a matrix with 10000 (or 100000 if you’re using a fast computer) columns, each containing 100 random numbers from a normal distributionThe function
system.time()will return the time taken by your computer to carry out an operation specified as an argument (e.g.system.time(mean(MyVector))will give you the time taken to calculate the mean of MyVector). Usesystem.time()to compare the time taken to calculate the means of every column in your giant matrix created above when you useapply()and when you usecolMeans. NBsystem.time()actually gives you three values, don’t worry too much about these (read the help file forproc.time()if you want to know more), just use the “elapsed” value.On the basis of what you’ve seen when comparing the efficiency of
colMeans()versusapply(), rewrite theboot.conf()function that we developed in the section onreplicate()so that it runs faster.
12.7 Solutions to exercises
- Load and attach the haemocyte data which we previously used in chapter 9
haemocyte<-read.table("Data/Haemocyte.txt",header=T)
head(haemocyte)
Species Weight Count
1 P.napi 0.0660 106.5
2 P.napi 0.0761 160.0
3 P.napi 0.1273 206.0
4 P.napi 0.0816 73.0
5 P.napi 0.0879 48.0
6 P.napi 0.1365 181.5
attach(haemocyte)- Use
apply()to calculate the overall mean for Weight and for Count
apply(haemocyte[2:3],2,mean)
Weight Count
0.18374 95.17797 - Use
tapply()to calculate the mean Weight and Count for both species. This will take two separate instructions.
tapply(Weight,Species,mean)
P.brassicae P.napi
0.28809 0.08286
tapply(Count,Species,mean)
P.brassicae P.napi
81.793 108.117 - Now use
aggregate()to calculate the mean Weight and Count for both species. You should be able to do this with just one instruction.
aggregate(haemocyte[2:3],by=list(Species=Species),mean)
Species Weight Count
1 P.brassicae 0.28809 81.793
2 P.napi 0.08286 108.117- Use
by()to return the intercept and slope for a regression of Count on Weight for the two species analysed separately
by(haemocyte, Species, function(x) lm(x$Count~x$Weight)$coefficients)
Species: P.brassicae
(Intercept) x$Weight
99.991 -63.167
------------------------------------------------------------
Species: P.napi
(Intercept) x$Weight
30.40 937.92 - Use
replicate()to generate a matrix with 10000 (or 100000 if you’re using a fast computer) columns, each containing 100 random numbers from a standard normal distribution
mat1<-replicate(10000,rnorm(100))- The function
system.time()will return the time taken by your computer to carry out an operation specified as an argument (e.g.system.time(mean(MyVector))will give you the time taken to calculate the mean of MyVector). Usesystem.time()to compare the time taken to calculate the means of every column in your giant matrix created above when you useapply()and when you usecolMeans.
system.time(apply(mat1,2,mean))
user system elapsed
0.056 0.003 0.058
system.time(colMeans(mat1))
user system elapsed
0.001 0.000 0.001 These are the times taken to carry out these operations on my computer, so yours will almost certainly be different. The basic pattern should be the same, though: colMeans() is much, much faster. The technical explanation for this is that it is a heavily optimised function with the main calculations running in machine code, whereas apply() is written in R throughout so it is much slower. If that’s a bit too geeky for you don’t worry, just remember that colMeans() (and its friends rowMeans(), colSums() and rowSums()) are very, very fast.
- On the basis of what you’ve seen when comparing the efficiency of
colMeans()versusapply(), rewrite theboot.conf()function that we developed in the section onreplicate()so that it runs faster.
To do this you need to replace the apply() function in the second line of code with a colMeans(). I’ve also changed the name of the function so that we can compare its performance with the original.
boot.conf.fast<-function(X1,conf=95) {
bootstrap.means<-colMeans(replicate(1000,sample(X1,size=length(X1),replace=TRUE)))
output<-c(quantile(bootstrap.means,(100-conf)/200),quantile(bootstrap.means,1-(100-conf)/200))
output
}test<-rnorm(100)
system.time(boot.conf.fast(test))
user system elapsed
0.013 0.000 0.013
system.time(boot.conf(test))
user system elapsed
0.027 0.000 0.028 The new version of our function takes roughly half the time to carry out this operation than the original.